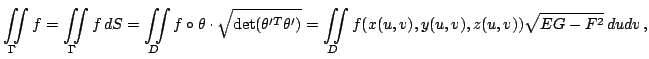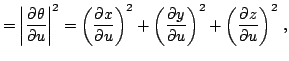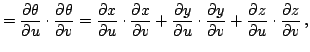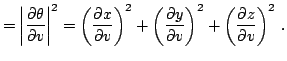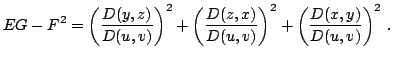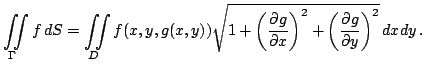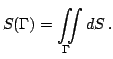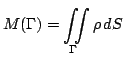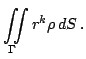Простая гладкая поверхность 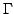 в
в
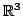 определяется как
множество значений гладкой функции
определяется как
множество значений гладкой функции
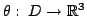 ,
определенной на некоторой связной жордановой области
,
определенной на некоторой связной жордановой области
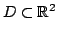 ,
при этом считается, что
,
при этом считается, что
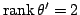 . Вектор-функция
. Вектор-функция 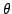 называется параметризацией поверхности
называется параметризацией поверхности 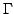 . Координаты на области
. Координаты на области 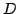 называются локальными координатами на поверхности
называются локальными координатами на поверхности 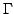 . В координатах
поверхность будет описываться равенствами
. В координатах
поверхность будет описываться равенствами
Интеграл от функции 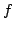 по поверхности
по поверхности 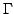 определяется равенствами
определяется равенствами
где
Имеет место также равенство
В случае явного задания поверхности 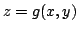
Определение интеграла по поверхности не зависит от параметризации.
Интеграл обладает свойствами линейности относительно подынтегральной функции
и аддитивности относительно поверхности интегрирования. Интеграл от
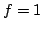 по поверхности
по поверхности 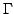 называется площадью поверхности
называется площадью поверхности
Физический смысл интеграла
-- масса поверхности 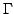 с плотностью
с плотностью 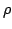 . Моменты k-го порядка
определяются аналогично со случаем криволинейного интеграла как
интегралы вида
. Моменты k-го порядка
определяются аналогично со случаем криволинейного интеграла как
интегралы вида
Александр Будылин
2004-08-30