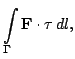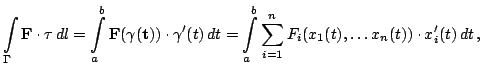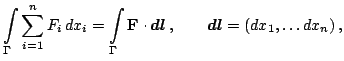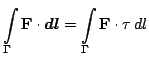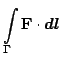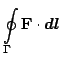Пусть 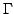 -- ориентированная кривая в
-- ориентированная кривая в
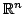 с параметризацией
с параметризацией
![$ \gamma (t) ,\;t\in[a,b]$](img201.gif) . Соответствующий единичный касательный вектор
обозначим через
. Соответствующий единичный касательный вектор
обозначим через 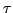 . Пусть
. Пусть
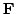 -- векторное поле, определенное
в точках кривой
-- векторное поле, определенное
в точках кривой 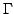 . Криволинейный интеграл 1 рода вида
. Криволинейный интеграл 1 рода вида
где
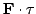 -- стандартное скалярное произведение векторов
в
-- стандартное скалярное произведение векторов
в
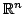 ,
называют криволинейным интегралом 2 рода. Ввиду
,
называют криволинейным интегралом 2 рода. Ввиду
 ,
,
где
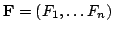 и
и
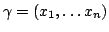 . Последний интеграл
записывают кратко как
. Последний интеграл
записывают кратко как
и называют интегралом от 1-формы
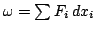 по кривой
по кривой 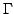 .
Равенство
.
Равенство
характеризуют как связь криволинейных интегралов 2-го и 1-го рода. Интеграл 2-го рода
зависит от ориентации кривой: при смене ориентации (
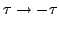 ) он меняет знак.
При фиксированной ориентации интеграл 2-го рода от параметризации не зависит.
) он меняет знак.
При фиксированной ориентации интеграл 2-го рода от параметризации не зависит.
Физический смысл криволинейного интеграла 2-го рода
-- работа силы
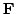 при перемещении вдоль пути
при перемещении вдоль пути 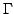 . Интеграл
по замкнутой кривой обозначают через
. Интеграл
по замкнутой кривой обозначают через
и называют циркуляцией поля
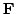 по ориентированной кривой
по ориентированной кривой 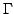 .
.
Александр Будылин
2004-08-30