Вперед: Примеры решения задач Выше: Поверхностные интегралы 2 рода Назад: Поверхностные интегралы 2 рода
Ориентация поверхности ![]() с параметризацией
с параметризацией
![]() , определяется ориентацией пространства локальных координат
, определяется ориентацией пространства локальных координат
![]() .
Эта ориентация может быть также определена как непрерывная ориентация
касательных пространств к поверхности
.
Эта ориентация может быть также определена как непрерывная ориентация
касательных пространств к поверхности ![]() (т.е. посредством задания
базиса касательных векторов, непрерывно зависящего от точки поверхности).
В случае гиперповерхности ориентация может быть задана при помощи
трансверсальной ориентации, т.е. посредством непрерывной ориентации
нормалей к гиперповерхности, с одновременным заданием ориентации
объемлющего пространства. Именно, гладкое нормальное векторное поле
(т.е. посредством задания
базиса касательных векторов, непрерывно зависящего от точки поверхности).
В случае гиперповерхности ориентация может быть задана при помощи
трансверсальной ориентации, т.е. посредством непрерывной ориентации
нормалей к гиперповерхности, с одновременным заданием ориентации
объемлющего пространства. Именно, гладкое нормальное векторное поле
![]() определяет ориентацию гиперповерхности с касательным базисом
определяет ориентацию гиперповерхности с касательным базисом
![]() , если вектора
, если вектора
![]() определяют ориентацию
определяют ориентацию
![]() .
.
Интеграл от ![]() -формы
-формы
![]() по множеству
по множеству ![]() в стандартно ориентированном
пространстве
в стандартно ориентированном
пространстве
![]() с формой объема
с формой объема
![]() определяется равенством
определяется равенством
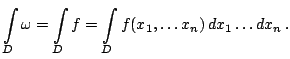 |
Интеграл от ![]() -формы
-формы ![]() по ориентированной
по ориентированной ![]() -мерной поверхности
-мерной поверхности ![]() с параметризацией
с параметризацией
![]() определяется равенством
определяется равенством
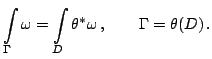 |
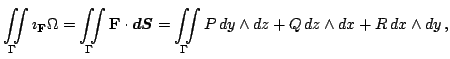 |
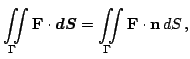 |
Физический смысл интеграла
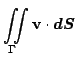 |
Александр Будылин