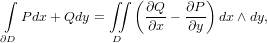
Ответ:
Формула Грина связывает интеграл по области от дифференциала 1-формы с интегралом по границе от самой 1-формы
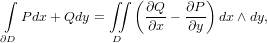 |
при этом, область и ее граница должны быть ориентированы согласованно, что
означает, что при обходе границы область должна лежать слева. Введем
единичный касательный вектор к границе  , где угол
, где угол  образован направлением вектора
образован направлением вектора  и осью абсцисс. Запишем криволинейный
интеграл 2 рода слева через криволинейный интеграл 1 рода и интеграл от
2-формы справа через двойной интеграл, получим
и осью абсцисс. Запишем криволинейный
интеграл 2 рода слева через криволинейный интеграл 1 рода и интеграл от
2-формы справа через двойной интеграл, получим
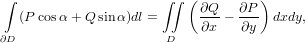 |
Заметим, далее, что вектор 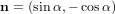 является вектором внешней
нормали к границе
является вектором внешней
нормали к границе 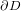 . Введем векторное поле
. Введем векторное поле 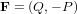 . Тогда формула
Грина перепишется в виде
. Тогда формула
Грина перепишется в виде
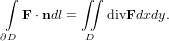 |
Это и есть требуемое равенство, поскольку обе его части уже не зависят от ориентации.