 и
и 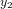 определяется
как функция вида
определяется
как функция вида
Ответ: Вронскиан двух дифференцируемых функций  и
и 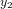 определяется
как функция вида
определяется
как функция вида
![| |
||y1 y2|| ′ ′
W [y1,y2] = |y1′ y′2| = y1(x)y2(x)- y2(x)y1(x).](ldu2wr2x.png) |
Если функции 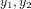 линейно зависимы, их вронскиан равен тождественно
нулю. Если эти функции являются решениями линейного однородного
дифференциального уравнения второго порядка
линейно зависимы, их вронскиан равен тождественно
нулю. Если эти функции являются решениями линейного однородного
дифференциального уравнения второго порядка
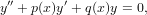 |
верно и обратное. Более того, если определитель Вронского решений этого уравнения равен нулю хотя бы в одной точке, то решения линейно зависимы. Если вронскиан решений не равен нулю хотя бы в одной точке, то он не равен нулю везде и решения будут линейно независимы на любом интервале в области непрерывности коэффициентов рассматриваемого уравнения.
Имеет силу также следующая формула Лиувилля
 |