 в пространстве
в пространстве 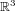 задается параметрически как
образ некоторого гладкого пути
задается параметрически как
образ некоторого гладкого пути ![γ(t),t ∈ [a,b]](soglornt2x.png) , в координатном виде:
, в координатном виде:
Ответ: Гладкая кривая  в пространстве
в пространстве 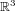 задается параметрически как
образ некоторого гладкого пути
задается параметрически как
образ некоторого гладкого пути ![γ(t),t ∈ [a,b]](soglornt2x.png) , в координатном виде:
, в координатном виде:
 |
Если  , край кривой пуст. В противном случае краем
, край кривой пуст. В противном случае краем 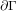 кривой
называется множество
кривой
называется множество 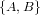 ее концов:
ее концов: 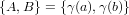 .
.
Ориентацию кривой можно определить выбором одного из двух единичных касательных векторов
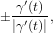 |
непрерывно зависящих от точки 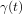 кривой. Под ориентацией края кривой
понимают упорядочение множества
кривой. Под ориентацией края кривой
понимают упорядочение множества 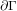 .
.
Если касательный вектор  задает ориентацию кривой
задает ориентацию кривой 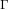 , то
согласованную ориентацию ее края
, то
согласованную ориентацию ее края 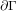 определяют как пару концов
определяют как пару концов 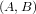 такую, что
такую, что 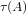 является внутренним по отношению к краю вектором,
т.е.
является внутренним по отношению к краю вектором,
т.е.  для точек
для точек 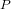 кривой, достаточно близких к точке
кривой, достаточно близких к точке
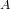 .
.