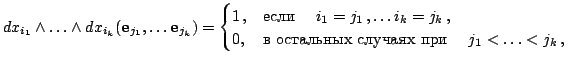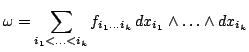Внешняя 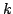 -форма в
-форма в
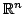 это
функция
это
функция 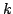 векторных аргументов
векторных аргументов
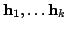 ,
линейно зависящая от каждого аргумента и антисимметричная. Последнее означает,
что
,
линейно зависящая от каждого аргумента и антисимметричная. Последнее означает,
что 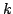 -форма обращается в ноль всякий раз, когда какие-либо два ее
аргумента совпадают. В условиях полилинейности это означает, что
-форма обращается в ноль всякий раз, когда какие-либо два ее
аргумента совпадают. В условиях полилинейности это означает, что
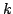 -форма меняет знак при перестановке местами двух аргументов.
Множество внешних
-форма меняет знак при перестановке местами двух аргументов.
Множество внешних 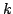 -форм образует линейное пространство с базисом
из форм
-форм образует линейное пространство с базисом
из форм
Последние определяются равенствами
где
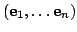 -- базис в
-- базис в
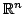 .
Дифференциальные
.
Дифференциальные 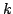 -формы это функции точки
-формы это функции точки
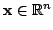 , принимающие
значения в пространстве внешних
, принимающие
значения в пространстве внешних 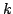 -форм. Таким образом, дифференциальная
-форм. Таким образом, дифференциальная
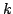 -форма
-форма 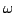 это внешняя форма
это внешняя форма
с функциональными коэффициентами
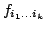 , зависящими
от
, зависящими
от
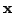 . Если
. Если
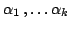 -- 1-формы,
через
-- 1-формы,
через
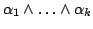 обозначается
обозначается 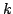 -форма,
определенная равенством
-форма,
определенная равенством
Такие формы называются мономами. По определению полагают
По линейности операция внешнего произведения 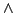 распространяется на произвольные формы,
при этом
распространяется на произвольные формы,
при этом
где 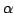 и
и 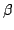 , соответственно,
, соответственно, 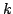 и
и 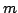 -формы.
-формы.
Александр Будылин
2004-08-30