Если 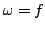 -- 0-форма, т.е. функция, то ее внешний дифференциал есть
1-форма
-- 0-форма, т.е. функция, то ее внешний дифференциал есть
1-форма
В общем случае внешний дифференциал 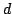 формы
формы 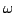 определяется равенствами
определяется равенствами
Имеют место соотношения
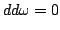 (лемма Пуанкаре) (лемма Пуанкаре) |
|
и
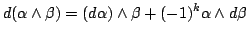 (правило Лейбница) (правило Лейбница) |
|
здесь 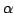 --
-- 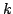 -форма.
-форма.
Форма
 получается из формы
получается из формы 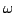 при
замораживании ее первого векторного аргумента на значении
при
замораживании ее первого векторного аргумента на значении
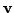 .
Таким образом, в случае монома,
.
Таким образом, в случае монома,
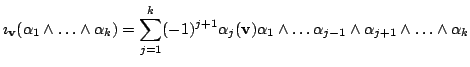 (разложение Лапласа) (разложение Лапласа)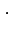 |
|
Операция
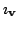 называется внутренним умножением формы
на вектор
называется внутренним умножением формы
на вектор
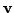 . Она подчиняется правилу Лейбница
. Она подчиняется правилу Лейбница
где 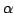 --
-- 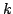 -форма.
-форма. 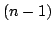 -форма
-форма
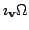 , где
, где
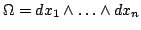 , называется формой потока вектора
, называется формой потока вектора
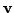 .
.
Операция
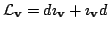 подчиняется правилу Лейбница
подчиняется правилу Лейбница
перестановочна с внешним дифференциалом
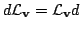 и называется производной Ли формы.
и называется производной Ли формы.
Александр Будылин
2004-08-30
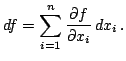
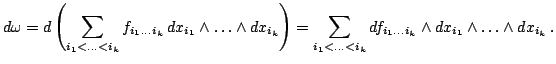
![]() получается из формы
получается из формы ![]() при
замораживании ее первого векторного аргумента на значении
при
замораживании ее первого векторного аргумента на значении
![]() .
Таким образом, в случае монома,
.
Таким образом, в случае монома,
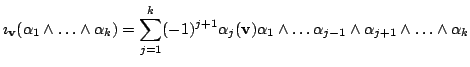 (разложение Лапласа)
(разложение Лапласа)![]() подчиняется правилу Лейбница
подчиняется правилу Лейбница