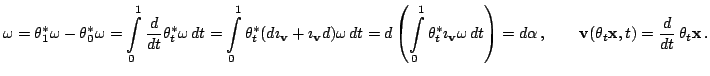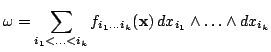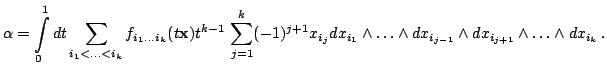Форма 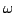 точна, если
точна, если
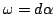 . Форма
. Форма 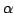 при этом
называется потенциалом или первообразной формы
при этом
называется потенциалом или первообразной формы 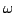 . В силу леммы Пуанкаре
потенциал определен не однозначно, а лишь с точностью до точной формы.
Форма
. В силу леммы Пуанкаре
потенциал определен не однозначно, а лишь с точностью до точной формы.
Форма 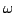 называется замкнутой, если
называется замкнутой, если 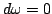 . Замкнутая форма не
обязана быть точной. Но
если отображение
. Замкнутая форма не
обязана быть точной. Но
если отображение
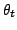 при изменении параметра
при изменении параметра 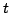 от
от 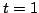 до
до 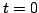 стягивает область
стягивает область 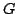 в точку
в точку
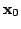 , то для замкнутой в
, то для замкнутой в 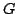 формы
формы 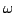 получаем представление
получаем представление
В частности,
замкнутая форма 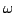 локально точна (теорема Пуанкаре). В окрестности нуля
потенциал замкнутой
локально точна (теорема Пуанкаре). В окрестности нуля
потенциал замкнутой 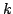 -формы
-формы
может быть построен по формуле
Александр Будылин
2004-08-30