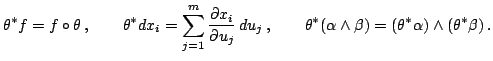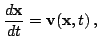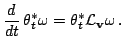Если 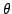 -- гладкое отображение
-- гладкое отображение
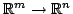 ,
определенное равенствами
,
определенное равенствами
 или, кратко,
или, кратко,
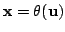 , то
, то
Если отображение 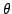 обратимо, то операцию
обратимо, то операцию
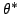 называют
заменой переменных в форме. В противном будем говорить о сужении
формы на поверхность, параметрически определенную отображением
называют
заменой переменных в форме. В противном будем говорить о сужении
формы на поверхность, параметрически определенную отображением 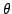 .
Имеет место равенство
.
Имеет место равенство
Если 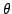 -- преобразование в
-- преобразование в
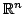 и
и
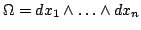 , то
, то
Если отображение
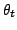 определяет эволюцию системы со скоростью
определяет эволюцию системы со скоростью
 , т.е.
функция
, т.е.
функция
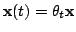 является решением дифференциального
уравнения
является решением дифференциального
уравнения
то имеет силу формула Картана
Александр Будылин
2004-08-30