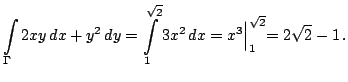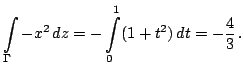Задача

Найти работу поля $\mathbf{F}=2xy\vec i+y^{2}\vec j-x^{2} \vec k$ вдоль кривой $\Gamma$

$$x^{2}+y^{2}-2z^{2}=2 ,\qquad y=x ,$$

от точки $A (1,1,0)$ до точки $B ( \sqrt{2},\sqrt{2},1)$ .

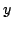
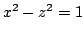
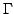
Решение. Исключая из уравнений переменную $y$ , придем к равенству $x^{2}-z^{2}=1$ . Это означает, что кривая $\Gamma$ может быть параметризована равенствами

$$x=\sqrt{1+t^{2}} ,\quad y= \sqrt{1+t^{2}} ,\quad z= t , \qquad t\in[0,1].$$

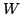
Тогда искомая работа $W$ равна

$$\begin{multline*} W=\int\limits_{\Gamma} \mathbf{F}\cdot \boldsymbol{dl}= \int\l... ...t^{3}}{3} \right]\Biggl\vert _{0}^{1}=2 \sqrt{2}- \frac{7}{3} . \end{multline*}$$

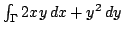
Отметим, что несколько более рационально было бы отдельно вычислить интеграл $\int_{\Gamma} 2xy dx+y^{2} dy$ , выбирая в качестве параметра $x$ :

$$\int\limits_{\Gamma}2xy dx+y^{2} dy= \int\limits_{1}^{\sqrt{2}} 3x^{2} dx=x^{3}\Bigl\vert _{1}^{ \sqrt{2}}=2 \sqrt{2}-1 .$$

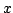
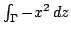
Оставшийся же интеграл $\int_{\Gamma}-x^{2} dz$ удобно вычислять с описанной выше параметризацией:

$$\int\limits_{\Gamma}-x^{2} dz= -\int\limits_{0}^{1} (1+t^{2}) dt=-\frac{4}{3} .$$

Полный ответ получается суммированием. $\qedsymbol$