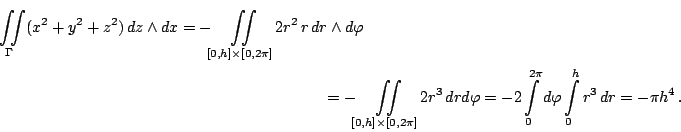Задача

Найти поток вектора $\mathbf{F}= (x^{2}+y^{2}+z^{2})\vec j$ через [боковую] поверхность конуса $y=\sqrt{x^{2}+z^{2}} ,\;0\leqslant y\leqslant h$ , ориентированную внешней нормалью.

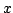
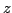
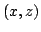
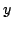
Решение. В качестве локальных координат на конусе можно было бы выбрать $x$ и $z$ . Согласование с заданной ориентацией диктует именно этот порядок локальных координат: $(x,z)$ (вектор внешней нормали составляет с осью $y$ тупой угол). Более удобно сразу воспользоваться переходом к полярным координатам. Таким образом, приходим к следующей параметризация поверхности $\Gamma$

$$x=r\cos\varphi ,\quad y=r ,\quad z=r\sin\varphi ,\qquad r\in[0.h],\quad \varphi \in[0,2\pi) ,$$

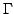
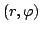
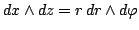
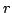
с ориентацией, определенной порядком $(r,\varphi)$ локальных координат (ввиду, например, равенства $dx\wedge dz= r dr\wedge d\varphi$ и положительности $r$ ). Тогда, искомый поток равен

$$\begin{multline*} \iint\limits_{\Gamma} (x^{2}+y^{2}+z^{2}) dz\wedge dx=- \iint... ...ts_{0}^{2\pi}d\varphi \int\limits_{0}^{h}r^{3} dr=-\pi h^{4} . \end{multline*}$$

$\qedsymbol$