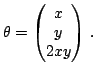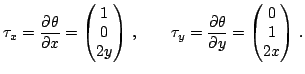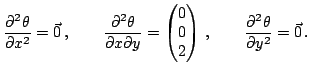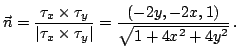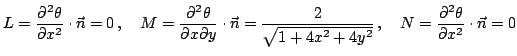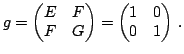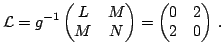Найти первую и вторую квадратичные формы поверхности 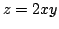 .
Вычислить ее среднюю и гауссову кривизну в точке
.
Вычислить ее среднюю и гауссову кривизну в точке 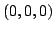 .
.
Решение:
В качестве локальных координат на поверхности выбираем 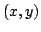 :
:
Находим касательные вектора:
Тогда
и первая квадратичнсая форма определена равенством
Вычислим, далее:
Найдем единичный нормальный вектор к поверхности:
Тогда
и вторая квадратичная форма определена равенством
В точке 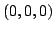 матрица метрического тензора равна
матрица метрического тензора равна
Тогда матрица отображения Вейнгартена равна
Средняя и полная кривизны в этой точке, соответственно, равны
Александр Будылин
2004-08-30
![]() :
: