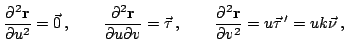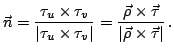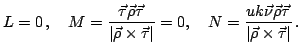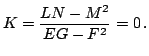Найти первую и вторую квадратичные формы поверхности. Вычислить ее
полную (гауссову) кривизну.
где 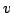 -- естественный параметр на кривой
-- естественный параметр на кривой
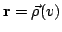 .
.
Решение:
Находим касательные векторы:
где 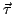 -- единичный касательный вектор к кривой
-- единичный касательный вектор к кривой 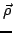 .
Тогда
.
Тогда
где
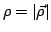 .
.
Далее,
где 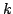 и
и 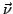 -- кривизна и вектор главной нормали к кривой
-- кривизна и вектор главной нормали к кривой 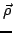 .
.
Найдем единичный нормальный вектор к поверхности:
Тогда
Полная кривизна
Александр Будылин
2004-08-30